U računalstvu i teoriji informacije, duljina kodne riječi označava broj znamenaka (bitova) u jednoj kodnoj riječi. Često se označava malim slovom l. Ona je vrlo bitno svojstvo kodne riječi. Generalno, preferiraju se kraće kodne riječi kako bi efikasnost koda bila što veća. [1]
Prosječna duljina kodne riječi
Prosječna duljina kodne riječi koristi se kod entropijskog neravnomjernog kodiranja. Često se označava velikim slovom L. Ona označava prosječan broj znamenaka (bitova) kodne riječi u danoj tablici kodnih riječi uzimajući u obzir vjerojatnost pojavljivanja kodnih riječi. Kod ravnomjernog kodiranja nema smisla govoriti o prosječnoj duljini koda zbog toga što je duljina svake kodne riječi jednaka. U takvom slučaju je prosječna duljina kodne riječi identična duljini jedne kodne riječi. Ona je bitan faktor koji utječe na efikasnost koda.
Prosječna duljina kodne riječi računa se kao ponderirana aritmetička sredina pojedinih kodnih riječi, tj. može se izračunati kao suma svih umnožaka duljina pojedinih kodnih riječi i njihovih pripadajućih vjerojatnosti. [2]
Prikazano sljedećom jednadžbom:
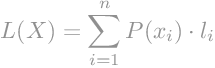 |
Pri čemu je:
- L(X) – prosječna duljina kodne riječi
- n – ukupan broj kodnih riječi
- P(xi) – vjerojatnost pojave i-tog simbola
- li – duljina i-te kodne riječi
Primjer računanja prosječne duljine kodne riječi
Zamislimo slikovnicu u kojoj se pojavljuju samo prva četiri slova engleske abecede. Iz slikovnice izračunamo vjerojatnost pojave pojedinih slova te zapišemo u tablicu. Zamislimo da je netko već uspješno iskodirao slova. Izračunajmo prosječnu duljinu kodne riječi.
| Simbol (xi) | Vjerojatnost pojave (P(xi)) | Kodna riječ | Duljina kodne riječi (li) |
| A | 1/2 | 0 | 1 | B | 1/6 | 10 | 2 |
| C | 1/6 | 110 | 3 |
| D | 1/6 | 111 | 3 |
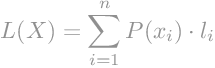 |
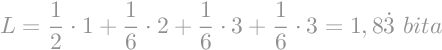 |
Prosječna duljina kodne riječi u ovome slučaju iznosi 1.83 bita.
Donja granica prosječne duljine kodne riječi
Ako govorimo o kodiranju bez gubitka informacija, onda je jasno da prosječna duljina kodne riječi ne može biti manja od entropije. Kada bi ona bila manja, kôd bi nosio manje informacija od samog izvora, što znači da se jedan dio informacija izgubio u procesu kodiranja. Iz toga slijedi da prosječna duljina kodne riječi mora biti veća ili jednaka entropiji. [3]
 |
Kompaktnost koda
Informacije je moguće kodirati na više različitih načina pa tako različiti kodovi imaju i različite duljine kodnih riječi.
Za neki kod možemo reći da je kompaktan, za jedan izvor, ako mu je prosječna duljina kodne riječi manja ili jednaka prosječnoj duljini svih ostalih kodova koji se mogu dekodirati na jedinstven način za taj isti izvor. [4]
Reference
1. Luenberger, David G. (2006). Information Science, str. 22. Princeton, New Jersey: Princeton University Press. ISBN 978-0-637-12418-3.
2. Togneri R., deSilva Christopher J.S. (2003). Fundamentals of Information Theory and Coding Design, str. 121. Boca Raton, Florida: CRC Press. ISBN 978-0-203-99810.
3. Togneri R., deSilva Christopher J.S. (2003). Fundamentals of Information Theory and Coding Design, str. 123. Boca Raton, Florida: CRC Press. ISBN 978-0-203-99810.
4. Togneri R., deSilva Christopher J.S. (2003). Fundamentals of Information Theory and Coding Design, str. 121. Boca Raton, Florida: CRC Press. ISBN 978-0-203-99810.