U računalstvu i teoriji informacije, Huffmanov kod je poseban prefiksni kod koji se najčešće koristi za sažimanje podataka bez gubitaka. Proces pronalaženja ili korištenja toga koda naziva se Huffmanovo kodiranje. Algoritam pomoću kojega se pronalazi kod, konstruirao je David Albert Huffman za vrijeme doktorskog studija na MIT-u. Svoje otkriće objavio je u radu “A Method for the Construction of Minimum-Redundancy Codes” 1952. [1]
Huffmanov kod je neravnomjeran kod. Algoritmom se dobiva tablica kodova koja se bazira na vjerojatnosti pojave svakog simbola pojedinačno, što znači da će simboli koji imaju veću vjerojatnost pojavljivanja biti kodirani s kraćim kodnim riječima, a simboli koji imaju manju vjerojatnost pojavljivanja biti kodirani s duljim kodnim riječima. Takvim načinom kodiranja povećava se efikasnost koda.
Huffmanovo kodiranje
Huffmanov algoritam
Huffmanov algoritam je algoritam pomoću kojeg se na jednostavan način može kodirati neka informacija. On nam govori sljedeće… [2]
- Posložimo vjerojatnosti od najveće prema najmanjoj, tako da se najveća vjerojatnost nalazi na krajnoj lijevoj strani, a najmanja na krajnjoj desnoj strani.
- Zbrojimo dvije krajnje desne vjerojatnosti.
- Zbrojimo dvije najmanje vjerojatnosti. U slučaju postojanja više jednakih najmanjih vjerojatnosti, zbrojimo bilo koje dvije, obično se zbrajaju dvije s krajnje desne.
- Ponavljamo korak 3 dok ne ostane samo jedna vjerojatnost. Ako je stablo ispravno, ona će uvijek biti jednaka 1.
- Počevši od vrha prema dnu, na svakoj točki na kojoj se stablo grana, dodijelimo po jednu binarnu vrijednost (0 ili 1) svakoj grani. Obično se lijevoj grani pridodaje 0 a desnoj 1. Ako se napravi obrnuto, kod će izgledati malo drugačije, ali će imati identična svojstva.
- Počevši od vrha, gibamo se najkraćim putem do prve vjerojatnosti, te pritom ispisujemo bitove na koje nailazimo, redom, s lijeva na desno. Ponavljamo za svaku vjerojatnost pojedinačno.
Primjer Huffmanovog algoritma
Zamislimo sljedeći slučaj. Meteorološka postaja nalazi se na otoku koji je 10 km udaljen od najbližeg grada na kopnu. U meteorološkoj postaji nalazi se osoba koja svaki dan, točno u podne, zabilježi vrijeme na pučini. Nakon toga u svome čamcu otplovi do grada te mještanima preda informaciju o vremenu na pučini. To je vrlo naporan posao, no na svu sreću, tehnološkom revolucijom, izumljen je uređaj koji ima mogućnost slanja električnih signala u grad, kroz žicu koju su postavili. Dogovoreno je slanje električnog signala koji predstavlja određeno vrijeme na pučini. Dogovorena su 4 različita vremena: sunčano, oblačno, maglovito te kišno. Kako bi poslali informaciju o vremenu s pomoću električnog signala, potrebno je svako vrijeme pojedinačno predstaviti nekim kodom koji se potom šalje električnim signalom. Uzmimo u obzir da su to bili sami početci tehnike pa je stoga svaki poslani signal (bit) bio jako skup. Iz toga razloga je bilo potrebno smanjiti broj signala koji se šalju. Bilo je potrebno pronaći najefikasniji kod. Iz dosadašnjih mjerenja izračunali su vjerojatnost pojave pojedinog vremena. Vjerojatnost sunčanog vremena je iznosila 1/2. Vjerojatnost oblačnog vremena je iznosila 1/6. Vjerojatnost maglovitog vremena je iznosila 1/6. Vjerojatnost kišnog vremena je iznosila 1/6. Vidimo da je vjerojatnost sunčanog vremena najveća, što znači da je veći dio godine sunčano vrijeme, te da će se ta informacija najčešće slati. Kako bi trošak bio najmanji, bilo bi logično signal koji se šalje najčešće predstaviti najkraćim mogućim kodom. Pitanje je, kako doći do najefikasnijeg koda?
Ovaj zadatak riješit ćemo pomoću Huffmanovog algoritma crtajući Huffmanovo stablo.
1. Posložimo vjerojatnosti od najveće prema najmanjoj, tako da se najveća vjerojatnost nalazi na krajnoj lijevoj strani, a najmanja na krajnjoj desnoj strani.
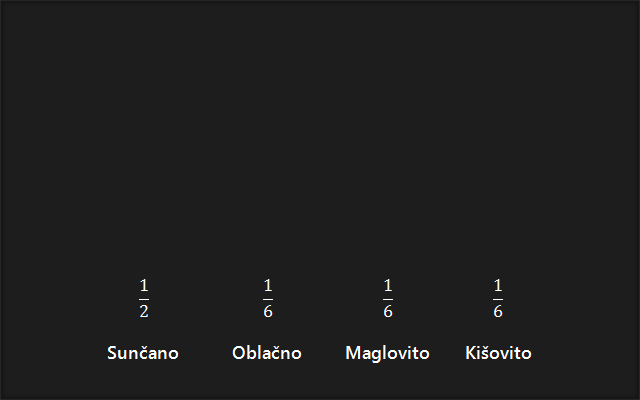
2. Zbrojimo dvije krajnje desne vjerojatnosti.
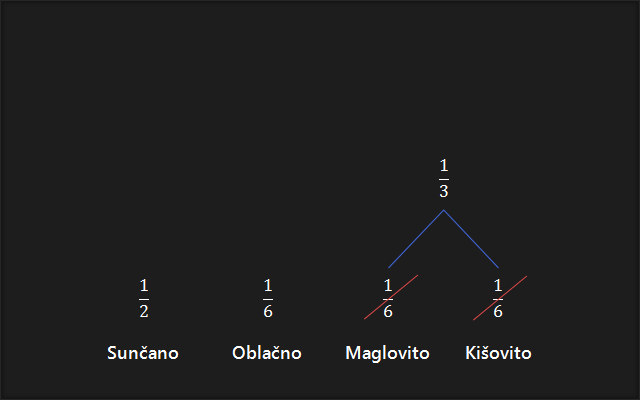
3. Zbrojimo dvije najmanje vjerojatnosti. U slučaju postojanja više jednakih najmanjih vjerojatnosti, zbrojimo bilo koje dvije, obično se zbrajaju dvije s krajnje desne.
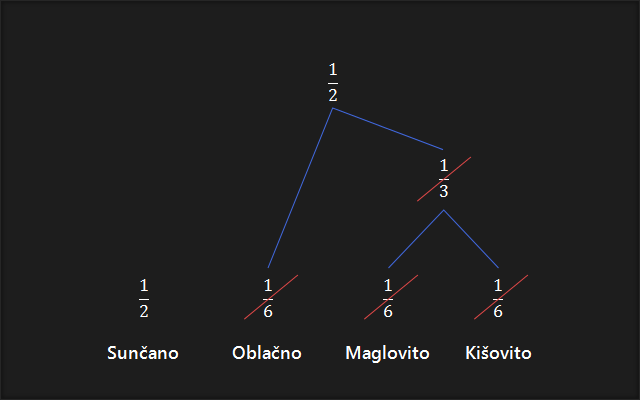
4. Ponavljamo korak 3 dok ne ostane samo jedna vjerojatnost. Ako je stablo ispravno, ona će uvijek biti jednaka 1.
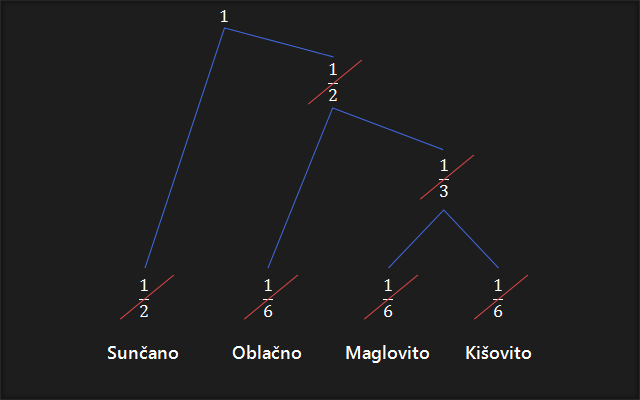
5. Počevši od vrha prema dnu, na svakoj točki na kojoj se stablo grana, dodijelimo po jednu binarnu vrijednost (0 ili 1) svakoj grani. Obično se lijevoj grani pridodaje 0 a desnoj 1. Ako se napravi obrnuto, kod će izgledati malo drugačije, ali će imati identična svojstva.
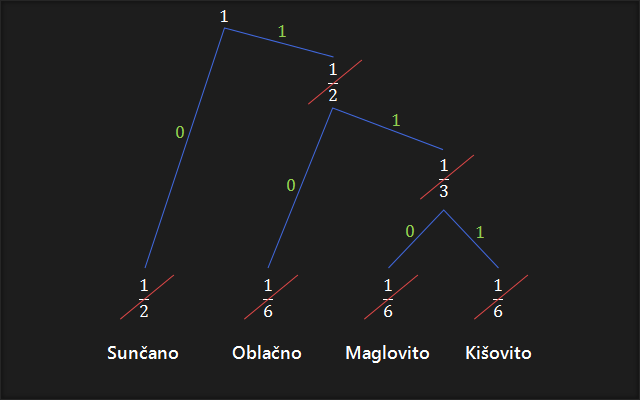
6. Počevši od vrha, gibamo se najkraćim putem do prve vjerojatnosti, te pritom ispisujemo bitove na koje nailazimo, redom, s lijeva na desno. Ponavljamo za svaku vjerojatnost pojedinačno.
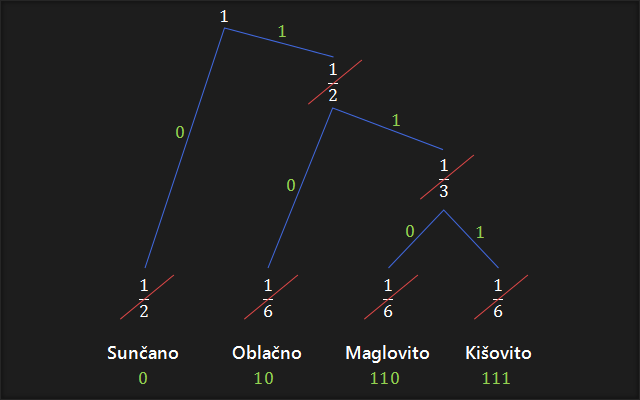
Ovime smo dobili najefikasniji kod za navedene vjerojatnosti.
Možemo izračunati efikasnost koda. Za efikasnost koda nam je potrebna entropija i prosječna duljina kodne riječi.
Entropiju izračunamo kao sumu svih pojedinačnih entropija.
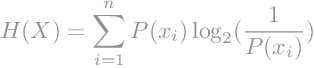 |
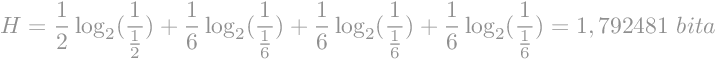 |
Prosječnu duljinu kodne riječi možemo izračunati kao sumu umnoška vjerojatnosti i duljine kodne riječi.
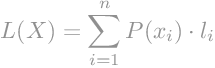 |
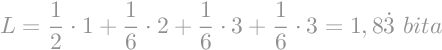 |
Efikasnost koda možemo izračunati kao omjer entropije i prosječne duljine kodne riječi.
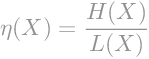 |
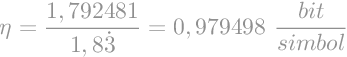 |
U ovome slučaju efikasnost koda iznosi približno 98%. Vidimo da je izračunata prosječna duljina kodne riječi samo malo veća od izračunate entropije. Tako da ne samo da je ovaj kod efikasan, on je ujedno i veoma blizu teoretskog limita kojeg je postavio Shannon.
Fleksibilnost Huffmanovog algoritma
Kako u prethodnom primjeru postoji više jednakih vjerojatnosti, zadatak smo mogli riješiti i na drugi način. Na primjer da smo prvo zbrojili vjerojatnosti za oblačno i maglovito vrijeme, a potom tu vrijednost s vjerojatnosti za kišno vrijeme. Kodne riječi bi bile u različitom poretku. Prosječna duljina kodne riječi bi ostala ista, a samim time i efikasnost.
U nekim slučajevima se može promijeniti i duljina kodne riječi. Promotrimo sljedeću tablicu.
| Vjerojatnost (pi) | Kod 1 | Kod 2 |
| 0,4 | 1 | 00 |
| 0,2 | 01 | 10 |
| 0,2 | 000 | 11 |
| 0,1 | 0010 | 010 |
| 0,1 | 0011 | 011 |
Oba koda su dobivena pomoću Huffmanova algoritma, međutim na prvi pogled izgledaju potpuno različito. Duljine kodnih riječi su različite. Uzmimo vjerojatnost 0,4, u prvom kodu duljina kodne riječi iznosi 1 bit, a u drugom kodu duljine kodne riječi iznosi 2 bita. Međutim ako bi izračunali prosječnu duljinu kodne riječi, ona bi u oba slučaja iznosila 2,2 bita što znači da bi efikasnost bila jednaka u oba slučaja. Huffmanov algoritam uvijek daje najefikasniji kod s najmanjom mogućom prosječnom duljinom kodne riječi za određeni skup vjerojatnosti, iako je moguće dobiti više naizgled različitih kodova. To upravo demonstrira fleksibilnost Huffmanovog algoritma. [3]
Huffmanovo dekodiranje
Huffmanov kod je kod s prefiksom što znači da postoji samo jedan način na koji se kodna riječ može dekodirati. Taj uvjet je osiguran zbog toga što ni jedna kodna riječ ne predstavlja prvi dio (prefiks) neke druge kodne riječi. Ako taj uvjet ne bi bio osiguran, onda bi jedno kodnu riječ mogli dekodirati na više različitih načina. Ispunjenje ovog uvjeta se jasno vidi na samom Huffmanovom stablu.
Proces dekodiranja je vrlo jednostavan. Prilikom dekodiranja se koristi prethodno izgrađeno Huffmanovo stablo, tako što čitamo kodne riječi bit po bit, pri čemu se počevši od vrha (korijena) spuštamo duž grana na kojima se nalaze pojedini bitovi, sve dok ne dođemo do simbola. Na ovaj način možemo potpuno rekonstruirati početni simbol pa stoga Huffmanov kod spada u grupu reverzibilnih kodova.
Sažimanje podataka
Statičko Huffmanovo kodiranje
Osnovna ideja Huffmanovog kodiranja je pridodijeliti kodne riječi najmanje duljine simbolima koji se najčešće pojavljuju. Iz tog razloga je za primjenu Huffmanovog kodiranja potrebno znati vjerojatnost pojave određenog simbola. Na temelju tih vjerojatnosti, u statičkom Huffmanovom kodiranju, Huffmanovo stablo se kreira na samom početku kodiranja te se više ne mijenja tijekom procesa. Međutim, ovo je ograničavajući faktor u mnogim primjenama. U slučajevima gdje nije moguće točno odrediti vjerojatnost pojave određenog simbola ili u slučajevima gdje se ona mijenja dinamički, primjena Huffmanovog koda neće dati najveće moguće sažimanje.
Uzmimo na primjer Hrvatski jezik. Znamo približno vjerojatnosti pojava određenih slova u hrvatskom jeziku. Pomoću tih vjerojatnosti možemo konstruirati Huffmanovo stablo te izvesti kodne riječi za pojedino slovo. Huffmanovim algoritmom dobijemo najkraće kodne riječi za slova koja se pojavljuju najčešće, tj. najdulje kodne riječi za slova koja se pojavljuju najrjeđe. Međutim, problem se javlja ako tu tablicu iskoristimo na dvije knjige različitih tematika. Recimo da se radi o znanstveno-fantastičnom romanu i znanstvenom radu iz područja elektrotehnike. Ako primijenimo naše stablo na znanstveno-fantastični roman, nećemo postići jednak stupanj sažimanja kao na znanstvenom radu. Razlog tomu je različita vjerojatnost pojave pojedinih slova. U znanstvenom radu će se možda češće pojavljivati slova U (napon), I (struja), R (otpor) nego u romanu.
Možemo reći da Huffmanov kod nije univerzalan kod što znači da neće dati najveću moguću kompresiju u svim primjenama, upravo zbog toga što je ovisan o poznavanju vjerojatnosti. Kako bi se nosili s time, razvijena je nova metoda Huffmanovog kodiranja, nazvana dinamičko ili adaptivno Huffmanovo kodiranje.
Dinamičko (adaptivno) Huffmanovo kodiranje
Kod dinamičkog (adaptivnog) Huffmanovog kodiranja, prilikom svakog novog kodiranja, vjerojatnosti pojave simbola računaju se dinamički, tijekom samog procesa kodiranja. To ipak nije najefikasnija metoda jer se kod takvog postupka Huffmanovo stablo stalno iznova mijenja pa takvo kodiranje ima veće vrijeme izvršavanja. Stoga se za npr., kodiranje teksta, koriste kodovi s manjim vremenom izvršavanja, poput Lempel-Ziv koda.
Primjena
Huffmanovo kodiranje se često koristi pri sažimanju podataka, npr. u DEFLATE algoritmu za sažimanje kojeg koriste mnogi programi sa sažimanje datoteka različitih vrsta poput .ZIP datoteka. [4] Huffmanovo kodiranje se također koristi u sažimanju .JPEG i .MP3 datoteka. [5] [6]
Reference
1. Huffman, David A. (1952). A Method for the Construction of Minimum-Redundancy Codes. Proceedings of the IRE, 40. svezak, 9. izdanje, str. 1098–1101. (PDF)
2. Togneri R., deSilva Christopher J.S. (2003). Fundamentals of Information Theory and Coding Design, str. 137. Boca Raton, Florida: CRC Press. ISBN 978-0-203-99810.
3. Luenberger, David G. (2008). Information Science. New Jersey: Princeton University Press. ISBN 978-0-691-12418-3.
4. PKWARE (2012). .ZIP File Format Specification, sekcija 5.5, Deflating – Method 8. (TXT)
5. CCITT (1993). INFORMATION TECHNOLOGY – DIGITAL COMPRESSION AND CODING OF CONTINUOUS-TONE STILL IMAGES – REQUIREMENTS AND GUIDELINES, str. 50. (PDF)
6. ISO/IEC 11172-3 (1993). Coding of moving pictures and associated audio for digital storage media at up to about 1,5 Mbit/s – Part 3.